numpyとscipyのヒストグラム

numpy.histogram()の仕様を自分用に和訳。

http://docs.scipy.org/doc/numpy/reference/generated/numpy.histogram.html

---

numpy.histogram(a, bins=10, range=None, normed=False, weights=None, density=None)

＃パラメータについて

a : array様シーケンス（おそらく普通のリストでもいいってことだと思う）
入力データ。aが二次元以上の場合、平坦化してから計算される。

bins : int もしくは尺のシーケンス（省略可）
intの場合、そのintは階級数(bins)の個数を規定する。（デフォルトで10階級）
シーケンスの場合、そのシーケンスの値は階級境界(bins edges)を規定する。ただし、最右端もそのシーケンスに含まれなければならない。非均等幅も可能。

range : (float, float) （省略可）
binsの最小と最大値。デフォルトでは、単純に(a.min(), a.max())が与えられる。

normed:
バグとか混乱が大きいため、numpy 2.0以降では廃止[なので訳さない。]

weights : array様シーケンス
重みの配列で、aと同じ形をしているシーケンスをとる。aのそれぞれの値は度数のカウントの際にその重み倍されて数えられる。

density : bool（省略可）
Trueにすると、度数の代わりにその階級での規定した幅の全面積が1になるような確率密度関数の値が出力される。単位幅(unity width)の階級が選ばれていない限り、度数の総和が1にならないことに注意。すなわち、確率質量関数ではない。[つまり、density=Trueにした場合は、得られた値×階級幅が相対度数になるのかな？まあ相対度数グラフならdensity=Falseで度数リストもらってから、それをデータ数で割ったほうが簡単そうだ。]

＃返り値

hist : array
度数。
bin_edges : array of dtype float
階級境界の値（最右端も含む）

-------------------------------------
scipy.stats.histogram()も存在した！
何が違うのかよくわからんので、とりあえず和訳。

http://docs.scipy.org/doc/scipy-0.14.0/reference/generated/scipy.stats.histogram.html

---

scipy.stats.histogram(a, numbins=10, defaultlimits=None, weights=None, printextras=False)
指定された範囲をいくつかの階級にわけ、それぞれの階級の度数を返す。

#パラメータ:

a : array様シーケンス
データの配列

numbins : int (省略可)
階級の数。デフォルトは10

defaultlimits : タプル (lower, upper) (省略可）
ヒストグラムの範囲の最小値と最大値。省略した場合は、データの範囲(max(a)-min(a))よりわずかに広めに範囲が設定される。
特に、(a.min() - s, a.max() + s),
ここで s = (1/2)(a.max() - a.min()) / (numbins - 1).

weights : array様シーケンス（省略可）
aのそれぞれの値に対する重み。デフォルトだと無し、すなわち、それぞれに1倍の比重をかける。

printextras : bool（省略可）
Trueにした場合、除外点(extra points)（設定した範囲から漏れたデータ）があるときにその数をprintする。デフォルトはFalse.


#返り値:

histogram : ndarray
それぞれの階級の度数（もしくは重み付き度数）

low_range : float
ヒストグラムの階級境界の最小値（最左端）。

binsize : float
階級幅(the size of the bins)。すべての階級は等幅である。

extrapoints : int
ヒストグラムの範囲から漏れたデータの個数

--------------------------------------
#どっちを使うべきなんだろう
とりあえず、numpyのほうは非均等階級幅が設定できるのが強み（？）でも使うことあんのか。
その自由性があるから階級境界値もシーケンスでリターンするんだね。
しかし、numpyのほうは最右端の値も度数としてカウントするという、データの階級への入れ方が非均等なのであまりすきじゃない。しかも、ヒストグラム書くときのルールである「階級境界はデータの0.5単位下にとる」というのをガン無視してるので。

そう考えると、scipyのほうがより正確。ヒストグラムの範囲をデータ範囲より若干広く取るので。さらに非均等幅の設定はできないので、返り値もシンプル。ただ、グラフ書くときはちょっとめんどくさそう。

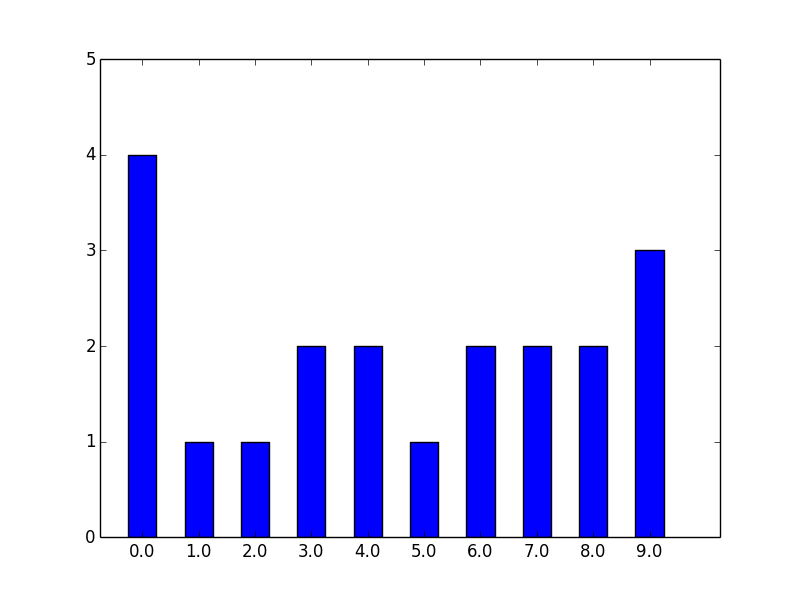
>>> data = np.random.randint(0,10,20)
>>> data
array([0, 2, 4, 9, 1, 0, 0, 6, 7, 8, 5, 3, 9, 7, 6, 3, 4, 9, 8, 0])
>>> stats.histogram(data)
(array([ 4.,  1.,  1.,  2.,  2.,  1.,  2.,  2.,  2.,  3.]), -0.5, 1.0, 0)
>>> his_f, his_amin, his_d = stats.histogram(data)[:-1]

諸々の値デフォルト（階級数10）で度数分布作ったの図。
階級境界最小値は-0.5, 階級幅は1.0から、ヒストグラムの横軸を作れるはず。

とりあえず、numpyの返り値である、bin_edgeの最右端の無いバージョンは、

>>> bin_edge = np.array([his_amin + his_d * i for i in range(np.size(his_f))])
array([-0.5,  0.5,  1.5,  2.5,  3.5,  4.5,  5.5,  6.5,  7.5,  8.5])

とすれば求まるし、階級値c(階級境界の中点)は、

>>> his_c = bin_edge + np.ones(np.size(his_f))*0.5*his_d
array([ 0.,  1.,  2.,  3.,  4.,  5.,  6.,  7.,  8.,  9.])

とすればよい。ここまでくれば、あとはnumpyと同様、

>>> pl.bar(his_c,his_f)

でおｋ。pl.xlim, pl.ylim, pl.xticks, pl.yticks などはお好みでどうぞ。

一例を下に。

import numpy as np
from scipy import stats as stats
import pylab as pl

data = np.array([0, 2, 4, 9, 1, 0, 0, 6, 7, 8, 5, 3, 9, 7, 6, 3, 4, 9, 8, 0])
bins = 10
his_f, his_amin, his_d =stats.histogram(data, numbins=bins)[:-1]
bin_edge = np.array([his_amin+his_d*i for i in range(bins)])
his_c = bin_edge + np.ones(bins)*0.5*his_d

bar_width = 0.5
pl.xlim(min(bin_edge)-0.5,max(bin_edge) + his_d + 0.5)
pl.ylim(0,max(his_f)+1)
pl.xticks(bin_edge + np.ones(bins)*bar_width*0.5, his_c)
pl.bar(bin_edge, his_f, width = bar_width)

xtickでx軸の目盛りは色々変えれるはず。

階級範囲を示しておきたい（普通はこれがベターかも）なら、


xticks_label = [str(i)+"~"+str(i+his_d) for i in bin_edge]
pl.xticks(bin_edge + np.ones(bins)*bar_width*0.5, xticks_label)


としてやれば、

みたいな感じでいけます。内包表記って便利だなあ！

numbinsはデフォルトで10ではあるが、実際は平方根則やらスタージェスの公式を使ったほうがいいかもしんないね！

グレた確率統計 ～ポアソン分布～

これまでにしてきたことを少し振り返ってみましょう。

まず、ベルヌーイ試行から始まりました。ONかOFFか、YESかNOか、1か0か、というやつですね。それを複数回行ったときのONの数の確率分布を求めました（二項分布）。そして、初めてONが出たときの試行回数の確率分布も求めました（幾何分布）。畳み込みを踏まえた上で、幾何分布の一般形、すなわち r回ONが出たときの試行回数の確率分布も求めました（負の二項分布）。そのあと、連続化に進み、幾何分布を連続化しました（指数分布）。また、負の二項分布の連続化、もしくは指数分布の畳み込みを行いました（アーラン分布）。

二項分布、幾何分布、負の二項分布、指数分布、アーラン分布が、単純なベルヌーイ試行から導出されてきたことを見てきたわけです。

さて、今回は、次のような分布を求めてみます。すなわち、「単位時間で事象がk回起こる確率」です。

最も単純明快な導出方法は、おそらく、アーラン分布（ガンマ分布）を用いたものでしょう。

単位時間で事象がk回起こる確率というのは、t' < 1 なる t' でk回起こり、残りの時間は起こらなかった確率と言い換えられます。t = t' で k回起こる確率というのはガンマ分布、

$$\Gamma(t; r=k) = \frac{t^{k-1} \phi^{k} \exp(-\phi t)}{(k-1)!}$$

で表わせ、残りの時間、すなわち t = 1-t' で1回も起こらない確率$g_0(t)$は指数分布を用いて、

$$g_0(t) = 1-\int_0^t \phi \exp(-\phi t') dt' = \exp(-\phi t)$$

とできますから、この2つの畳込み、

$$Pr(X=k) = \int_0^1 \Gamma(t';r=k)\cdot g_0 (1-t')dt' \\ = \int_0^1 \frac{t'^{k-1} \phi^{k} \exp(-\phi t')}{(k-1)!} \cdot \exp(-\phi (1-t')) dt' \\ = \frac{\phi^k \exp(-\phi)}{(k-1)!} \int_0^1 t'^{k-1}dt' = \frac{\phi^k}{k!}  \exp(-\phi) $$

この分布をポアソン分布といい、意味としてはさきに書いた通り、「単位時間で事象がk回起こる確率」となります。

というわけで、主要な確率分布が以上のようにすべて繋がっているように考えられるということが分かります。

（多分おしまい）

グレた確率統計 ～ガンマ・アーラン分布～

前回は、幾何分布から指数分布へ、つまり離散型から連続型への変換をやりました。
幾何分布は畳み込むことで負の二項分布になりましたね。
もちろんのことながら、負の二項分布を連続化した分布も考えることができます。
さらに言えば、指数分布を畳み込むことで同じ分布が得られるはずです。
それこそがガンマ分布（厳密に言えばアーラン分布）なわけです。

そこで、ここではガンマ分布を2つのやり方
① 負の二項分布の連続化
② 指数分布の畳み込み
で導出してみます。

① 負の二項分布の連続化

負の二項分布は、
$$Pr(X=k) = ~{}_{k-1} \mathrm{C}_{r-1} ~ p^r q^{k-r}$$
と表わせ、「事象が試行k回目にちょうどr回生じる確率」の意味付けができます。
これを連続化すれば、おそらく
「事象が時間tのときにちょうどr回生じる確率分布」が得られるはずです。

まず、組み合わせの変形はそのままではやりづらいので、負の二項分布の自然対数を変形していくことにします。
また、非常に大きい数 x について、スターリンの近似式、
$$ \ln x! \approx x \ln x - x$$
が成り立つこと、そして、小さい数 x について、次の近似式が成り立ちます：
$$ \ln (1-x) \approx -x $$
$$\ln Pr(X=k) = \ln \left( ~{}_{k-1} \mathrm{C}_{r-1} ~ p^r q^{k-r} \right) = \ln \left( \frac{(k-1)!}{(k-r)! (r-1)!} ~ p^r q^{k-r} \right ) \\ = \ln{(k-1)!} ~- \ln(k-r)! ~-\ln(r-1)! ~+ r\ln p + (k-r)\ln q $$

スターリンの式で、$\ln(k-1)!$と$\ln(k-r)!$を近似し、$p=\phi dt$を代入すると

$$= (k-1)\ln(k-1)-(k-1) - (k-r)\ln(k-r) +(k-r) -\ln(r-1)!+r \ln(\phi dt)+(k-r)\ln(1-p)$$

ここで、次の近似、
$$\ln(k-a)=\ln k + \ln(1-a/k) \approx \ln k - \frac{a}{k} \\\ln(1-p) \approx -p = -\phi dt$$
を使うと、
$$= (k-1)\left(\ln k-\frac{1}{k}\right) - (k-r)\left(\ln k -\frac{r}{k}\right) +1-r -\ln(r-1)!+r \ln(\phi dt)-(k-r)\phi dt\\= (r-1)\ln k -\frac{1}{k} ((k-1)-r(k-r)) + 1-r -\ln(r-1)!+ r\ln\phi +r\ln dt -\phi t+r\phi dt$$
少し式が煩雑になってきたので、
$L = -\ln(r-1)!+r\ln\phi-\phi t$と置いて、式を整理していくと、
$$=(r-1)\ln k -\frac{1}{k} ((k-1)-r(k-r)) + 1-r +r\ln dt+r\phi dt + L\\=(r-1)(\ln t - \ln dt)-\frac{1+r^2}{k}+r\ln dt + r\phi dt +L\\=(r-1)\ln t + \ln dt - \left(\frac{(1+r)^2}{t} +r\phi \right )dt + L$$
ここで、Lというのは、
$$L = \ln \left( \frac{\phi^r \exp(-\phi t)}{(r-1)!}  \right )$$
と変形できるので、これを使って変形すると、
$$= \ln \left( \frac{t^{r-1} \phi^r \exp(-\phi t)dt}{(r-1)!} \right) - \left(\frac{(1+r)^2}{t} +r\phi \right )dt\\ \approx \ln \left( \frac{t^{r-1} \phi^r \exp(-\phi t)dt}{(r-1)!} \right) ~~(\because dt \ll 1)$$

よって、
$$Pr(T=t) = \frac{t^{r-1} \phi^r \exp(-\phi t)}{(r-1)!} dt$$
となり、$Pr(T=t) = \Gamma (t) dt $とすれば、確率密度 Γ(t) は、
$$ \Gamma (t) = \frac{t^{r-1} \phi^r \exp(-\phi t)}{(r-1)!} $$
となります。

② 指数分布の畳み込み

t秒後にちょうどk回起こる確率分布を$g_k(t)$とすると、k=2のときは2つの指数分布をたたみ込めばいいので、

$$g_2(t)=\int_0^t \left(\phi \exp(-\phi (t-t')) \right )\left(\phi \exp(-\phi t') \right )dt'\\ = \phi^2 \exp(-\phi t) \int_0^t ~dt' = t \phi^2 \exp(-\phi t)$$

となります。一応$g_3(t)$も求めてみると、これは$g_2(t)$と指数分布の畳み込みで求められ、

$$ g_3(t) = \int_0^t g_2(t') \phi \exp(-\phi(t-t')) dt' \\ = \int_0^t t' \phi^3 \exp(-\phi t) dt' = \frac{t^2 \phi^3 \exp(-\phi t)}{2!} $$

となります。

ここから帰納的に、

$$ g_k(t) = \frac{t^{k-1} \phi^k \exp(-\phi t)}{(k-1)!} $$

と仮定してみると、

$$g_{k+1}(t) = \int_0^t g_k(t') \phi \exp(-\phi(t-t'))dt' \\ = \int_0^t \frac{t'^{k-1} \phi^k \exp(-\phi t')}{(k-1)!} \cdot \phi \exp(-\phi(t-t')) dt' \\ = \frac{\phi^{k+1} \exp(-\phi t)}{(k-1)!} \int_0^t t'^{k-1} dt' = \frac{\phi^{k+1} \exp(-\phi t)}{(k-1)!} \cdot \frac{t^k}{k}\\ = \frac{t^k \phi^{k+1} \exp(-\phi t)}{k!} $$

ということで、やはりどちらの側からもガンマ分布が求められました。
ちなみに今回出した分布のパラメータ r は正の整数値をとりますが、実際のガンマ分布のパラメータ r は正の実数値を取ります。

そこで、正の整数値をとる場合の確率分布はアーラン分布と呼ばれています。ですから、これら一連の導出は厳密にはアーラン分布の導出ということになります。

さて、ガンマ分布の平均値と分散を求めてみましょう。愚直に計算してもいいのですが、どうせなら、負の二項分布を連続化、もしくは指数分布を畳み込んだものがガンマ分布ということを利用してみましょう。

負の二項分布の平均値と分散はそれぞれ、$\mu = r/p,~~ \sigma^2 = rq/p^2$となります。
ここに、変数変換 $T = X dt$を考慮しながら、 $p = \phi dt$ を代入すれば、
$$ E(T) = E(X dt) = E(X) dt = \frac{r dt}{p} = \frac{r}{\phi} \\ Var(T) = Var(X dt) = Var(X) dt^2 = \frac{r q dt^2}{p^2} = \frac{r}{\phi^2} $$
と求められます。

また、ガンマ分布に従う確率変数 Z と r個の指数分布に従う変数 $X_i$ は、
$ Z = X_1 + X_2 + ... + X_r$
であり、かつ、$X_i$ はそれぞれ独立なので、
$E(Z) = E(X_1 + X_2 + ... + X_r) = E(X_1) + E(X_2)+ ... + E(X_r) = r/\phi$
分散も同様に、
$Var(Z) = Var(X_1 + X_2 + ... + X_r) = Var(X_1) + Var(X_2)+ ... + Var(X_r) = r/\phi^2$
と求められます。

定義通りに求めるやり方は、練習問題としておきます。

グレた確率統計 ～指数分布の補足～

さて、前回の幾何分布と指数分布について少し補足したいと思います。


指数分布の導出過程で、
$$p = \frac{dt}{\mu}$$
と置きましたね。すなわち、ここでpは「微小時間間隔 dt で事象が起こる確率」となっています。
これは、T = X dt と置いたことからも分かります。
この式を少し眺めていると、

[確率] = [確率密度] × [微小時間]

の形に見えてきませんか？つまり、pと対応する確率密度 $\phi$ を、

$$ p = \phi dt $$
$$ \phi = p / dt = 1/\mu $$

と定義してやることができます。これを指数分布に代入してみると、
$$f(t) = \frac{1}{\mu}\cdot \mathrm{exp}(-t/\mu) = \phi \cdot \exp(-\phi t)$$
となります。指数分布の離散版ともいえる幾何分布が、
$$Pr(X=k)= pq^{k-1} ~~~ (p+q=1)$$
だったことを考えると、qの累乗と、指数部に対応付けがしたくなります。

具体例を考えてみると、たとえば幾何分布では、
$$Pr(X \geq  k) = 1 - \sum_{i=1}^{k}p(1-p)^{i-1} \\ = 1 - p\cdot\frac{1-q^{k}}{1-q} = 1- (1-q^k) = q^k$$
であり、これに対応する指数分布の場合を考えると、
$$Pr(T \geq  t) = 1 - \int_{0}^{t} \phi \exp(-\phi t') dt'\\= 1 - [-\exp(-\phi t')]_0^t = 1- (1- \exp(-\phi t)) = \exp(-\phi t)$$
となり、
$$q^k = \exp(-\phi t)$$
と関連づけれそうです。
導出過程のことを考えると、tにとって k と k-1 はほとんど変わらないので、
$$ f(t) = \phi \cdot \exp(-\phi t) $$
というのは、幾何分布において、
$$p \rightarrow \phi$$
$$q^{k-1} \rightarrow \exp(-\phi t)$$
と置き換えたものだとみれます。

もうひとつ、q と exp(-φt) の対応付けが妥当な例を見てみましょう：
$$ q^{k-1} = (1-p)^{k-1} = (1-\phi dt)^k = (1-\phi dt)^{t/dt} = \exp(-\phi t)$$
ここで、$1/({1-\phi dt}) \approx 1$, $k = t/dt$ を用いました。
最後の等式は、指数分布の導出でも用いた、ネイピア数の定義です。

ということで、幾何分布と指数分布の形式的な対応付けが与えられたことになります。
その結果、期待値と分散も幾何分布から指数分布への簡単な対応付けで得られるはずです。

基礎分子物理化学 - KEITH A. McLAUCHLAN

　
名前の通り、物理化学の基礎のテキストですが、巻末を抜いてなんと１３１ページしかない。
この本は副読本という立ち位置を狙っているそうで、確かにそのような内容。

普通物理化学というと、まずは熱力学なわけだが、この本はアプローチが異なる：

今日では原子や分子の存在及び特性は確立されており、個々の原子や分子に対して実験ができるようになっている。これにより、実験対象をこれまでと違った見方をすることができ、原子や分子の特性から、それら集合体の特徴的なふるまいを導き出せるようになる。これは、化学の学校レベルの教え方としてふさわしいと言える。

こういった分子論から物理化学を始めていく教科書は他にもたくさんあるが、まずこのテキストは量子論史に沿っていない。よく出てくるリュードベリ定数も出てこないし、光電効果やプランクの式も冒頭に出てこない。本書はまず、「原子・分子の熱容量（エネルギー）には何が関係してくるのだろうか」ということから始める。ゆえに、まず出てくる数式は原子の平均エネルギー（ ＜E＞ = 3/2 kT)である。

そう考えると、本書は物理化学というよりは統計力学かもしれない。よく知られた量子力学の法則・定理・公式を素直に上げ、それらを用いて実測値は説明できるのかどうか、という視点からはじまる。

量子力学に真っ向から挑みたい人にはつまらないこと必至であるが、分光学、エネルギーの話等々、やや実学的に量子力学の役割を学ぶにはもってこいのテキストだと思う。

有効核電荷とイオン化エネルギー

イオン化エネルギーとは、ある原子の最外殻電子を自由電子にするのに必要なエネルギーのことで、その電子のおおよそのエネルギーの目安になります。元々電子をN個持っている原子について、N個の電子をN-1個にするエネルギーを第一イオン化エネルギー、N-1個をN-2個にするエネルギーを第二イオン化エネルギー…といいます。

以下、イオン化エネルギーのことをIEと呼ぶことにし、第nイオン化エネルギーのことをIEnと書くことにします。

wikipedia からデータを引っ張ってきてみると、

リチウムでは、

IE1 = 520.2 kJ/mol

IE2 = 7298.1 kJ/mol

IE3 = 11815 kJ/mol

となっており、一般的にIE1は一番低い値となります。

イオン化エネルギーの見積もりに使える式としては、水素型原子の軌道関数から出されたエネルギー準位、

$$E_n = - \frac {Z^2me^4} {32\pi^2 \epsilon_0^2 \hbar^2 n^2} = E_H \left( \frac{Z}{n} \right)^2$$

があります。ここで、$E_H$は水素原子の基底状態のエネルギーで、1312 kJ/mol に相当します。

しかし、実際に、多電子が軌道に入ると、自分以外の電子による核の遮蔽が起こるので、有効核電荷というものを考えなければなりません。これは、遮蔽定数Sを用いると、

$$Z_{eff} = Z - S$$

と書けます。遮蔽定数が大きいほど、他電子による影響が大きいということになります。

この有効核電荷（遮蔽定数）の概算規則として、スレーターの規則があります：

A. 着目する電子より外側の軌道に関しては無視する。

B. 着目する電子と同じグループにあるほかの電子からの寄与は電子1つにつき0.35（例外として1s軌道のときだけ0.30）とする。

C. 着目する電子がsとpのグループにあるときは、主量子数が1小さい電子からの寄与を電子1個につき0.85とし、その他の内側の電子の寄与は電子1個につき1.00とする。

これで、リチウムの有効核電荷を求めてみると、$1s^22s^1$ですから、

$$Z_{eff} = 3 - 0.85*2 = 1.3$$

となります。これにより、第一イオン化エネルギーは、

$$IE1 = 1312 \cdot \left( \frac{1.3}{2} \right)^2 =  554 kJ/mol$$

となります。実測値が520 kJ/mol であることを考えると、なかなかの精度です。

しかしながら、フッ素で同様な計算を行うと、

$$Z_{eff} = 9 - (6*0.35 + 0.85*2) = 5.2$$

$$IE1 = 1312 \cdot \left( \frac{5.2}{2} \right)^2 =  5869 kJ/mol$$

となりますが、実測値は1681kJ/mol であり、あまり精度がいいとは言えません。

そこで、完全に経験的に、遮蔽定数の新規則と、多電子原子におけるエネルギーを考えてみました。

■遮蔽定数の新規則

A. 着目する電子より外側の軌道に関しては無視する。

B. 着目する電子と同じ主量子数 n をもつ軌道にいる他の電子からの寄与は、

電子１つにつき $ 0.7 - 0.02n $

C. 着目する電子よりも主量子数が1小さい軌道にいる電子からの寄与は電子1個につき 0.86とし、それよりも内側の電子の寄与は電子1個につき 1.13とする

D. p軌道において、着目する電子がいる軌道にもう一つ電子が入っているとき（スピン量子数以外の量子数の組が同じ電子がいるとき）、0.42を足す

これで計算をしてみると、リチウムの有効核電荷は、

$$Z_{eff} = 3 - 0.86*2 = 1.28$$

よって、第一イオン化エネルギーは、

$$IE1 = 1312 \cdot \left( \frac{1.28}{1} \right)^2 =  537 kJ/mol$$

となり、スレーター規則よりも実測値に近くなります。

■多電子原子におけるエネルギーの新式

さきほどの、水素型原子のエネルギー式

$$E_n = - \frac {Z^2me^4} {32\pi^2 \epsilon_0^2 \hbar^2 n^2} = E_H \left( \frac{Z}{n} \right)^2$$に少し修正を加えた、

$$E_n = E_H \left( \frac{Z-S}{n+0.25nl} \right)^2$$

を考えてみます。ここで、$l$は方位量子数です。

この新しい概算式でフッ素のIE1をもう一度求めてみますと、

$$Z_{eff} = 9 - (0.42 + 0.86*2 + 0.66*6) = 2.9$$
$$IE1 = 1312 \cdot \left( \frac{2.9}{2+0.5} \right)^2 =  1765 kJ/mol$$

となり、スレーターの規則を用いたより断然いい値になります。

この精度はヘリウムのような、エネルギー式を修正しない場合でも発揮します。

スレーターの規則では、$Z_{eff} = 1.7$ ですが、新規則では$Z_{eff} = 1.32$となり、

それぞれからIE1を求めると、3791, 2286 kJ/mol となります。

実測値は2372 kJ/mol ですから、新規則のほうがいい精度です。

■何が違うのか

1つ違いの軌道間による遮蔽増加は、0.85, 0.86 とほとんど同じ値になっています。

２つの規則で大きく違うのは、同軌道での遮蔽増加、p電子反発項の２つです。

同じ軌道での遮蔽増加は、スレーターでは0.35, 新規則では 0.68 程度です。

この約2倍の違いが何の差を表しているのかは、ちょっとわかりません…。

そこで、おそらく、より妥当には、新規則を有効核電荷近似規則とするのではなく、
スレーターの規則によって求められた有効核電荷をさらに弱める不安定項の規則とすべきしょう。

その観点から、もう一度、新規則を整理しなおしてみます。

■IEにおける有効核電荷への調整項（他の因子によるエネルギーの不安定化）
これを$S'$と書くことにすると、イオン化エネルギーは、
$$IE = IE_H \left( \frac{Z-S-S'}{n+0.25nl} \right)^2$$
となる。ここで、Sはスレーターの規則により求められる遮蔽定数である。

$S'$は次の規則に従って求められる：

A. 着目する電子より外側の軌道の電子からは影響を受けない。

B. 着目する電子と同じ主量子数 n をもつ軌道にいる他の電子からの寄与は、

電子１つにつき 0.35 - 0.02n 。ただし、1s軌道に関しては 0.35

C. 着目する電子よりも主量子数が1小さい軌道にいる電子からの寄与は電子1個につき 0.01 とし、それよりも内側の電子の寄与は電子1個につき 0.13 とする

D. p軌道において、着目する電子がいる軌道にもう一つ電子が入っているとき（スピン量子数以外の量子数の組が同じ電子がいるとき）、0.42

こうすると、同軌道内での不安定化が0.3くらいになるので、スレーターの規則と比べても自然です。
有効核電荷はあくまで「どれだけ核が小さく（弱く）見えるか」を表すだけであって、
実際のその電子のエネルギーについて説明するパラメータではありません。
ですから、電子のエネルギーについてより正確な値がほしいときは、有効核電荷に不安定修正項を加える必要がありそうなことは想像できます。

有効核電荷は一般には同周期では番号が上がるにつれ大きくなっていきます。
それにより、安定化が望めるわけですが、実際の電子のエネルギーはというと、
それに加えて、いわば「他電子による押し出し」によるエネルギー増大が考えられます。
これを有効核電荷次元に換算した値がS'だと言えそうです。
それを踏まえて考えてみると、同主量子数からの「押出し」が大きく、
その下の主量子数からはあまり「押し出さ」れないということが推察できます。
また、p軌道において、スピン違いの電子がいるときは、大きな電子反発が起こることにより、イオン化エネルギーが下がると考えられます。

一応、実測値と理論値をArまでグラフで示しておきます。

グレた確率統計 ～指数分布～

今までは離散分布だけを扱ってきました。
ここでひとつ、幾何分布を連続化させてみましょう。
というのも、幾何分布の意味するところは「何かが起こるまでにかかる回数」なわけですが、
これを「何かが起こるまでにかかる時間」とするのはかなり有意義そうだからです。

まず、幾何分布は、
$$ Pr(X=k) = p q^{k-1}$$
で、期待値と分散は、
$$ E[X] = \frac{1}{p}$$
$$ Var[X] = \frac{q}{p^2}$$
となりましたね。

ここで、時間確率変数 T を微小量 $\Delta t$ を用いて、$T = \Delta t \cdot X$ と定義しましょう。
そうすると、幾何分布はtと $\Delta t$ で書き換えられて、

$$ Pr(T=t)= Pr(\Delta t \cdot X = t) = Pr(X = t/\Delta t) = pq^{(t/\Delta t) -1} $$

となります。ここで、Tの期待値を求めてみると、
$$\mu = E[T]=E[X\Delta t]=\Delta t \cdot E[X]=\frac{\Delta t}{p} $$
となります。

次に、p を $\mu$ で表すと、
$$p = \frac{\Delta t}{\mu}$$
となります。これを先ほどの分布の式に代入してやると、
$$ Pr(T=t)= \frac{\Delta t}{\mu}~\left(1-\frac{\Delta t}{\mu}\right)^{(t/\Delta t) -1} $$

さて、連続分布なので、確率密度関数を
$$f(t) = \frac{Pr(T=t)}{\Delta t}$$
で定義すると、

$$ f(t) = \frac{1}{\mu}~\left(1-\frac{\Delta t}{\mu}\right)^{(t/\Delta t) -1}\\
= \frac{1}{\mu (1-(\Delta t/\mu))}\left( \left(1-\frac{\Delta t}{\mu} \right )^{-\mu/\Delta t}\right)^{-t/\mu} \\
\xrightarrow[]{\Delta t \rightarrow 0} \frac{1}{\mu}\cdot \mathrm{exp}(-t/\mu)$$

この最後の式、
$$f(t) = \frac{1}{\mu}\cdot \mathrm{exp}(-t/\mu)$$
は指数分布といい、もちろんのことながら、「何かが起こるまでにかかる時間」の確率分布です。

期待値と分散は（導出は練習問題としましょう！）
$$ E[X] = \mu $$
$$ Var[X] = \mu ^2 $$
さらに、指数分布も幾何分布と同様、無記憶性を持っています（これも練習問題としましょう）。

グレた確率統計 ～忌まわしき組み合わせ（補遺）～

次の記事から、いよいよ離散分布から連続分布へ移っていきます。
そのターニングポイントとして、ここで天下り的に用いた３つの組み合わせの公式（とその補題）を、
ここで示しておこうかと思います。
というのは、
1. 負の二項定理（？）
$$\sum_{r=0}^\infty {}_{n+r-1}\mathrm{C}_{r}~x^r = (1-x)^{-n}$$

2.
$${ }_{n+m}\mathrm{C}_k =\sum_{l = k-\mathrm{min}(k,m)}^{\mathrm{min}(k,n)} { }_n\mathrm{C}_l \cdot { }_m\mathrm{C}_{k-l}$$

3.
$${}_{m}\mathrm{C}_{m}+  {}_{m+1}\mathrm{C}_{m}+{}_{m+2}\mathrm{C}_{m}+...+{}_{n}\mathrm{C}_{m}= { }_{n+1}\mathrm{C}_{m+1}$$

そして、パスカルの三角形を数式で表した、
4.
$${}_{n}\mathrm{C}_{m} = { }_{n-1}\mathrm{C}_{m} + { }_{n-1}\mathrm{C}_{m-1}$$

を補題とし、計４題を示していきたいと思います。

# 1. の証明
これは、$\frac{1}{(1-z)^n}$を級数展開してみればよい。
まずは、導関数を求める。
$$\frac{\mathrm{d} }{\mathrm{d} x} (1-z)^{-n} = n(1-z)^{-n-1}\\
\frac{\mathrm{d^2} }{\mathrm{d} x^2} (1-z)^{-n} =\frac{\mathrm{d} }{\mathrm{d} x} n(1-z)^{-n-1} = n(n+1)(1-z)^{-n-2}\\$$
これより、帰納的に
$$\frac{\mathrm{d}^k }{\mathrm{d} x^k} (1-z)^{-n} = n(n+1)...(n+k-1)(1-z)^{-n-k}=\frac{(n+k-1)!}{(n-1)!}(1-z)^{-n-k}$$
と分かる。
これを用いてz = 0 のまわりで級数展開すると、
$$(1-z)^{-n} = \sum_{k=0}^\infty \frac{(n+k-1)!}{(n-1)!~k!} z^k = \sum_{k=0}^\infty { }_{n+k-1}\mathrm{C}_{k}\cdot z^k$$
ここで、この級数の収束半径を求める。第k項を$a_k$と書くとすると、
ダランベールの収束判定法を用いて、
$$\left| \frac{a_{k+1}}{a_k} \right| = \left| \frac{n+k}{k+1}~ z \right| \xrightarrow[]{k \rightarrow \infty} |z| $$
よって、収束半径は $|z| < 1$ である。zが確率であるならば、$0 \leq z \leq 1$であるから、自明な場合の多い z = 1 を除けば、この等式は常に成り立つ。

# 2. の証明
$$(1+x)^{n+m} = \sum_{k=0}^{n+m} { }_{n+m}\mathrm{C}_{k} \cdot x^k\\
(1+x)^n (1+x)^m = \left( \sum_{i=0}^{n} { }_{n}\mathrm{C}_{i} \cdot x^i \right ) \left( \sum_{j=0}^{m} { }_{m}\mathrm{C}_{j} \cdot x^j \right )$$

$(1+x)^{n+m} = (1+x)^n (1+x)^m$ であるから、$x^k$の係数は、
(左辺) $$= { }_{n+m}\mathrm{C}_{k}$$
(右辺) $$=\sum_{\substack{i+j = k \\ 0 \leq i \leq n \\ 0 \leq j \leq m}} { }_{n}\mathrm{C}_{i} \cdot { }_{m}\mathrm{C}_{j}$$
$0 \leq k \leq m+n$より、これはすなわち
$$= \sum_{i = \mathrm{max}(k-m,0)}^{\mathrm{min}(n,k)} { }_{n}\mathrm{C}_{i} \cdot { }_{m}\mathrm{C}_{k-i}$$
であるので、題意は満たされた。ちなみに、
$$k-\mathrm{min}(k,m) = k + \mathrm{max} (-k, -m) = \mathrm{max}(0, k-m) $$
となる。

# 4. の証明
まずは補題として，パスカルの三角形を証明します。

$${ }_{n-1}\mathrm{C}_{m} + { }_{n-1}\mathrm{C}_{m-1} = \frac{(n-1)!}{(n-m-1)!~m!}+\frac{(n-1)!}{(n-m)!~(m-1)!}\\
=(n-1)!~\frac{(n-m)+m}{(n-m)!~m!} = \frac{n!}{(n-m)!~m!} = { }_{n}\mathrm{C}_{m}$$

# 3. の証明
少し書き換えた
$${}_{m}\mathrm{C}_{m}+  {}_{m+1}\mathrm{C}_{m}+{}_{m+2}\mathrm{C}_{m}+...+{}_{m+n}\mathrm{C}_{m}= { }_{m+n+1}\mathrm{C}_{m+1}$$
を数学的帰納法で証明する。

i) n = 0のとき、
$${}_{m}\mathrm{C}_{m}= { }_{m+1}\mathrm{C}_{m+1}$$
より明らか。

ii) n = k が成り立つと仮定すると、n = k + 1のとき、
$${}_{m}\mathrm{C}_{m}+  {}_{m+1}\mathrm{C}_{m}+{}_{m+2}\mathrm{C}_{m}+...+{}_{m+k}\mathrm{C}_{m}+{}_{m+k+1}\mathrm{C}_{m} \\
= {}_{m+k+1}\mathrm{C}_{m+1} + {}_{m+k+1}\mathrm{C}_{m}$$
ここで、4. の等式を使うと、
$${}_{m+k+1}\mathrm{C}_{m+1} + {}_{m+k+1}\mathrm{C}_{m} = {}_{m+(k+1)+1}\mathrm{C}_{m+1}$$
よって、n = k + 1 でも成り立つ。

これより、$n \geq 0$ で 3. は示された。

グレた確率統計 ～負の二項分布再考～

前回は、畳み込みとそれを用いた再生性についてやりました。
二項分布には再生性がある、ということでしたね。
さて、それでは、幾何分布には再生性はないのでしょうか？

# 幾何分布と畳み込み

幾何分布に従う独立な確率変数２つの和を確率変数とする分布を求めてみましょう。

幾何分布は、

$$Pr(X=k)=pq^{k-1}$$

でしたね。

さて、独立な２つの確率変数、XとYを用意して、それらはそれぞれ

$$Pr(X=i)=pq^{i-1}$$

$$Pr(Y=j)=pq^{j-1}$$

とします。

そこで、新たな確率変数$Z=X+Y$を定義して、$Pr(Z=k)$ を求めてみようということです。

$$Pr(Z=k)= \sum_{l=1}^{k-1} Pr(X=l)Pr(Y=k-l) \\ = \sum_{l=1}^{k-1} pq^{l-1} \cdot pq^{k-l-1} = (k-1)p^2 q^{k-2}$$

どうやら、幾何分布には再生性は無いようです。

しかし、これは、負の二項分布のr=2に相当します！

どういうことかというと、新しい確率変数Zの意味するところが、

「事象がちょうど2回起こるのにかかる試行回数」だからです。

それでは、「事象がちょうど3回起こるのにかかる試行回数」は、というと、

$W = Z + G_1$ (ここで$G_1$は幾何分布に従う確率変数) なる $W$を定義すると、

$$Pr(W=k)= \sum_{l=1}^{k-1} Pr(W=l)Pr(G_1=k-l) \\ = \sum_{l=2}^{k-1} (l-1)p^2 q^{l-2} \cdot pq^{k-l-1} = p^3 q^{k-3} \frac{(k-2)(k-1)}{2}$$

となり、やはり、負の二項分布のr = 3 に相当します。

さあ、任意のrな負の二項分布に従う確率変数Xと、幾何分布に従う確率変数Yの和として定義した確率変数Zがr+1な負の二項分布に従うことを示しましょう。

負の二項分布は
$${}_{k-1}C_{r-1}~p^{r}(1-p)^{k-r}$$
でしたね。

$$Pr(Z=k)= \sum_{l=r}^{k-1} Pr(X=l)Pr(Y=k-l) \\ = \sum_{l=r}^{k-1} {}_{l-1}C_{r-1}~p^{r}q^{l-r} \cdot pq^{k-l-1} \\ =p^{r+1} q^{k-(r+1)} \sum_{l=r}^{k-1} {}_{l-1}C_{r-1} $$

ここで、
$$\sum_{l=r}^{k-1} {}_{l-1}C_{r-1}$$
は、$$ x = l -r$$と置くと、
$$\sum_{l=r}^{k-1} {}_{l-1}C_{r-1} = \sum_{x=0}^{k-r-1} {}_{x+r-1}C_{r-1}$$

組み合わせの公式に、
$${}_{m}\mathrm{C}_{m}+  {}_{m+1}\mathrm{C}_{m}+{}_{m+2}\mathrm{C}_{m}+...+{}_{n}\mathrm{C}_{m}= { }_{n+1}\mathrm{C}_{m+1}$$
があるので、これを用いると、結果的に、
$${ }_{k-1} \mathrm{C}_{r}~p^{r+1} q^{k-(r+1)}$$

が得られます。これはやはり、負の二項分布のr=r+1に相当しますね！

ということで、n個の幾何分布に従う確率変数の和はr=nの負の二項分布に従うわけです。

これは、モーメント母関数からも割と明らかで、
幾何分布に従う独立な確率変数、$X_1, X_2, ... , X_n$の和であるような確率変数Yのモーメント母関数は、
$$M_Y(t) = E[e^{t(X_1+X_2+X_3+...+X_n)}]=E[e^{tX_1}]E[e^{tX_2}]...=\\
\left(\frac{pe^t}{1-qe^t} \right )\left(\frac{pe^t}{1-qe^t} \right )\left(\frac{pe^t}{1-qe^t} \right )... =\left(\frac{pe^t}{1-qe^t} \right )^n$$
なわけですから、確かに幾何分布n個から成り立ってるなあと思えます。

ちなみに、二項分布に従う独立な確率変数、$X_1, X_2, ... , X_n$の和であるような確率変数Yのモーメント母関数は、
$$M_Y(t) = E[e^{t(X_1+X_2+X_3+...+X_n)}]=E[e^{tX_1}]E[e^{tX_2}]...\\
= (q+pe^t)^{n_1} (q+pe^t)^{n_2} (q+pe^t)^{n_3}... = (q+pe^t)^{n_1+n_2+n_3+...}$$
となるため、確かにモーメント母関数にも再生性が見られます。


このように、畳み込みを使うことで、より一般的な分布を導出することが可能なわけです。

# 少しの意味付け

上では、幾何分布を畳み込むことの動機を「再生性を確かめる」としましたが、

もう少し、応用的な側面で幾何分布を畳み込みたくなりましょう。

一旦、負の二項分布のことは忘れて（！）、幾何分布だけ知っている状態に戻りましょう！

すなわち、「初めて事象Hが起こるときの試行回数がk であるような確率」は知っているとします。

そして、「事象Hがちょうど2回起こるときの試行回数がkであるような確率」を求めてみましょう。

しかし、その前に、具体例を以って理解しておくことにします。

ex) 確率$p$で事象Hが起こるようなベルヌーイ試行がある。

このとき、事象Hが10回目でちょうど2回起こる確率はいくらか。

まず、この場合の幾何分布は、

$$Pr(X=k) = p \cdot q^{k-1}$$

となります。さて、10回目の時点でちょうど2回起こるというのは、

「10回目までのどこかで1回起こり、そして10回目でもう1回起こった」ということです。

「どこか」とはどこでもいいわけで、例えば、3回目で1回、１０回目でもう１回というような確率は、

$$ p q^2 \cdot p q^6$$

となります。ここで大事なのが、２回目が１０回目で生じたというのは、４回目を２度目の開始点とし、そこから数えて７回目にHが生じたということです。

「どこか」は他にもあって、

* １回目と１０回目（２回目から始めて９回目）

* ２回目と１０回目（３回目から始めて８回目）

* ３回目と１０回目（４回目から始めて７回目）

…

と全部で9つあります。これらをすべて足しあわせたものが答えになります。つまり、

$$ Pr (X=10) = \sum_{i=1}^9 p q^{i-1} \cdot p q^{(10-i)-1} $$

ここに畳み込みが現れているのが分かりますね。

この結果はr = 2 の負の二項分布で k=10 としたものと同じになるのは上で求めたとおりです。

これを踏まえると、単に10をkに置き換えれば、一般化できますね。

このように、ごく素朴に幾何分布を使って「k回目にちょうどr回起こる確率」を求めることができます。

グレた確率統計 ～畳み込みと再生性～

さて、前回は負の二項分布についてやりました。
負の二項定理なるものが出てきて、計算もやや煩雑で、うんざりしかけましたね。
今回は、畳み込みと、それを利用した再生性の問題について考えていきましょう。
結構重要ですが、本筋と関係ないといえば関係ありません。

# 畳み込み

畳み込みとは、簡単にいえば、

「$x + y = k$ の$x,y$を少しずつ変化させながら、足していく」という作業です。

なんじゃそりゃと思うかもしれませんが、確率の問題を解く際に無意識のうちに使っています。

ex1)

同様に確からしいサイコロ２つを投げる。その和が8となるような確率を求めよ。

ふつうに解いてみると、和が8となるような組み合わせは、

(2,6), (3,5), (4,4) の3通りで、サイコロは区別されるので、5/36 ですね。

少し丁寧な言い回しで解いてみましょう。

サイコロの出る目の確率変数をそれぞれ$X,Y$とします。

さて、今回求めるべき確率は、$Pr(X+Y = 8)$ですね。

XとYは独立ですから、これは、

$$\sum_{k=1}^6Pr(X=k)Pr(Y=8-k)$$

と書くことができます。はい、畳み込んでますよね！

一般的に、$Pr(X+Y = n)$を求めるとしても、やはり、

$$\sum_{k=1}^6Pr(X=k)Pr(Y=n-k)$$

とするだけです。これは、「２つのサイコロの目の和の確率分布」ですね。

そうすると、「２つのサイコロの目の和」という確率変数を導入したくなります。

これは、$Z = X+Y$ とおいてやればいいわけで、結局、

$$Pr(Z=n) = Pr(X+Y = n) = \sum_{k=1}^6Pr(X=k)Pr(Y=n-k)$$

ということです。

「複数の確率変数の和を新たな確率変数で表すとき」、畳み込みという操作がでてくるわけです。

# 二項分布の畳み込みと再生性

懐かしの二項分布に戻ってきましょう。
コインをn回投げて、表（H)の出る回数 X を調べていたとします。
そして、後日、また同じコインをm 回投げて、表の出る回数 Y を調べたとしましょう。
さて、この２つの実験を合わせた、表の出た回数 $i+j$ はどんな分布に従うでしょうか。

もちろん、$Z = X + Y$ と置きます。
また、それぞれの分布は、
$$Pr(X=i) = { }_n\mathrm{C}_i~p^iq^{n-i}\\
Pr(Y = j) = { }_m\mathrm{C}_j~p^jq^{m-j}$$
となります。さて、この２つの分布は独立ですから、
$$Pr(Z = n) = \sum_{k = 0}^n Pr(X=k)Pr(Y = n-k)$$
となります。
（総和の上限を n としたのは、別に $\infty$にしてもいいのですが、$k > n$ のときでは$Pr(Y=n-k）=0$ですから、結局足さなくてもいいわけです。）

ざくざく計算を進めてみましょう。
$$Pr(Z = k) = \sum_{l = 0}^k Pr(X=l)Pr(Y = k-l)\\
=\sum_{l = 0}^k { }_n\mathrm{C}_l~p^lq^{n-l} \cdot { }_m\mathrm{C}_{k-l}~p^{k-l}q^{m-(k-l)}\\
= p^k q^{n+m-k}\sum_{l = 0}^k { }_n\mathrm{C}_l \cdot { }_m\mathrm{C}_{k-l}$$
ここで、気をつけてほしいのが、 $k > n+m$ では確率は0であることです。
すなわち、上の計算は $0 \leq k \leq n+m$ に限っています。
さらに言うと、 $k > min(n,m)$ のとき、組み合わせCが未定義な項が生じます(${ }_nC_{n+1}$ とか)。
このような場合も確率は0となりますから、除外しています。
ですから、もう少し厳密に式を書くと、
$$ \mathrm{if}~k>n+m, Pr(Z=k)=0,\\
\mathrm{else}~Pr(Z=k) = p^k q^{n+m-k}\sum_{l = k-\mathrm{min}(k,m)}^{\mathrm{min}(k,n)} { }_n\mathrm{C}_l \cdot { }_m\mathrm{C}_{k-l} $$

さて、$\sum_{l = k-\mathrm{min}(k,m)}^{\mathrm{min}(k,n)} { }_n\mathrm{C}_l \cdot { }_m\mathrm{C}_{k-l}$ですが、
これは、$(n+m)$個の選択肢の中から$k$個選ぶときの場合の数は、選択肢を$n$個と$m$個に分け、$n$個のほうから$l$個、$m$個のほうから$k-l$個選ぶ、というのを$l$の取り得る範囲で行い、それぞれでの場合の数をすべて足すことによっても求められるということを意味しています。
きちんと証明したい人は、数学的帰納法で証明してください。読者への(ry

結局！
$$ \mathrm{if}~k < n+m, Pr(Z=k)=0,\\ \mathrm{else}~Pr(Z=k) = p^k q^{n+m-k}{ }_{n+m}\mathrm{C}_k$$
となるわけです。これは、二項分布の形ですね。

すなわち、独立な二項分布に従う２つの確率変数の和はやはり二項分布に従うということです。
このように独立な同分布に従う２つの確率変数の和が同じ分布に従うことを再生性があると言います。

グレた確率統計 ～負の二項分布～

さて、前回は二項分布と幾何分布についてやりました。
とはいえ、大本はベルヌーイ試行（0か1か）でしたね。
それぞれの意味合いは、
* 二項分布 : n回試行したときに、事象Hがk回起こる確率の分布
* 幾何分布 : 事象Hが初めて起こるのがk回目である確率の分布
でしたね。

ここから脇道に逸れるとすれば、多項分布もありますが、
ここでは伏線にもなりうる負の二項分布をやりたいと思います。

# 負の二項分布

負の二項分布は、幾何分布の拡張とも言えます。
すなわち、「事象Hがちょうどr回起こるのがk回目である確率」です。
これは、k-1 回目まででHが r-1 回起こり、k回目でHが起こる確率です。
少し考えれば容易に立式できて、
$$
Pr(X=k)= {}_{k-1}C_{r-1}~p^{r-1}(1-p)^{(k-1)-(r-1)}\cdot p \\
=  {}_{k-1}C_{r-1}~p^{r}(1-p)^{k-r}
$$
となります。
ただし、k < r のときは、Cが定義されないので、0とします。
計算上は、(k-1)回試行の二項分布で、k = r-1としたものに pをかけた形となっています。
もちろんのことながら、r = 1 とすると幾何分布になりますね。

形としては、二項分布と幾何分布の間の子…みたいな感じになりますね。

さて、期待値と分散を求めようと思うのですが、一旦立ち止まって考えてみましょう。
幾何分布、すなわち1回事象Hが起こる回数の期待値は$1/p$ でした。
単純に考えると、r回起こる回数の期待値は$r/p$のような気がしますね。
もちろん、負の二項分布の場合もモーメント母関数を使って、
平均と分散を出せるのですが、…天下り的に負の二項定理なる、
$$
\sum_{r=0}^\infty {}_{n+r-1}\mathrm{C}_{r}~x^r = (1-x)^{-n}
$$
を飲み込んでもらう必要があります。
これを飲み込んでもらうとして、モーメント母関数を求めると、
$$
M_X{(t)} = E[e^{tX}] = \sum_{k=r}^\infty {}_{k-1}C_{r-1}~e^{tk}p^{r}(1-p)^{k-r}
$$
ここで、$m = k-r$とおくと、${}_{s+t}\mathrm{C}_s = {}_{s+t}\mathrm{C}_t$、例の公式より、
$$
\sum_{k=r}^\infty {}_{k-1}C_{r-1}~e^{tk}p^{r}(1-p)^{k-r} \\
= \sum_{m=0}^\infty {}_{m+r-1}C_{r-1}~e^{t(m+r)}p^{r}(1-p)^{m}\\
= (pe^t)^r \sum_{m=0}^\infty {}_{m+r-1}C_{m}~(qe^t)^m\\
=(pe^t)^r\cdot(1-qe^t)^{-r}= \left( \frac{pe^t}{1-qe^t} \right )^r
$$
と求まります。なんと、これは幾何分布のモーメント母関数のr乗ですね！
幾何分布のモーメント母関数を$f_{(t)}$と表すことにすると、
$$
M_X(t)=(f{(t)})^r
$$
なわけですから、幾何分布のところで求めたモーメント母関数の計算結果を利用しつつ、

* 平均
$$
E[X] = \frac{\mathrm{d} }{\mathrm{d} t}M_X(t) \\
= r(f(t))^{r-1}\cdot f'(t)|_{t=0} = \frac{r}{p}
$$

* 分散
$$
E[X^2]=\frac{\mathrm{d^2} }{\mathrm{d} t^2}M_X(t) = \frac{\mathrm{d} }{\mathrm{d} t}\left( r f'(t)(f(t))^{r-1} \right)\\
= rf''(t)(f(t))^{r-1}+r(r-1)\left(f'(t) \right )^2 (f(t))^{r-2}|_{t=0} \\
=\frac{r(2-p)}{p^2}+\frac{r(r-1)}{p^2}
$$
$$
\therefore Var(X)=\frac{r(2-p)}{p^2}+\frac{r(r-1)}{p^2}-\left( \frac{r}{p} \right )^2 = \frac{r(1-p)}{p^2}
$$

となります。
予想通り（？）、平均も分散も幾何分布のr倍となっていますね！

※ 補足 ---- ここから ----
ある分布 f, gのモーメント母関数をそれぞれ $M_f(t),~M_g(t)$ とし、
$$
M_g(t)=(M_f(t))^n
$$
のようにn乗の関係にあるとき、
$$
E_g[X] = \frac{\mathrm{d} }{\mathrm{d} t}M_g(t) = n(M_f(t))^{n-1}\cdot {M_f}'(t)|_{t=0} = n{M_f}'(0) = E_f[X]
$$
$$
E_g[X^2]=\frac{\mathrm{d^2} }{\mathrm{d} t^2}M_g(t) = \frac{\mathrm{d} }{\mathrm{d} t}\left( n {M_f}'(t)({M_f}(t))^{n-1} \right)\\
= n{M_f}''(t)({M_f}(t))^{n-1}+n(n-1)\left({M_f}'(t) \right )^2 ({M_f}(t))^{n-2}|_{t=0}\\
= n{M_f}''(0) + n(n-1)\left({M_f}'(0) \right )^2
$$
$$
\therefore Var_g(X) = n{M_f}''(0) + n(n-1)\left({M_f}'(0) \right )^2 - \left(n{M_f}'(0)\right)^2\\
= n({M_f}''(0)-{M_f}'(0)) = n\cdot Var_f(X)
$$
と、平均、分散がそれぞれn倍になります。

---- ここまで ----

少し長くなったので、ここで一旦終わります。

グレた確率統計 ～二項分布と幾何分布～

（ここに、”確率とはなにか”というのがいるとは思うのですが、前提知識としておきます）
（期待値、分散、モーメント母関数の定義はwikipediaに任せます）

# 二項分布

「二項」と言うくらいですから、コインの裏表のように「２つの事象」のどちらかが生じるような試行を考えます。コインになぞらえて、２つの事象をそれぞれH(head)とT(tail)と呼ぶことにします。
各試行は独立とします。このような試行をベルヌーイ試行と言うそうです。
さて、ベルヌーイ試行をn回行ったとき、Hがk回生じる確率は、

$$
Pr(X = k) = {}_n \mathrm{C}_k p^k (1-p)^{n-k} = \frac{n!}{(n-k)! k!} p^k (1-p)^{n-k}
$$

となるのは高校出てたら分かるでしょう！
もちろん、これは $ k : 0 \to \infty $ まで足し合わせると、1になるのは読者への演習(ry

概形はおおよそこんな感じになります。

0.3の確率で当たるなら、10回繰り返せば3回くらい出るだろうというのは間違ってないのがわかります。



一応、期待値と分散を求めておきましょう。（以下、適宜 $ q = 1-p $と書きます）
そのために、モーメント母関数を求めると、

$$
M_X (t) = E[e^{tX}] = \sum_{k=1}^n {}_n\mathrm{C}_k~e^{tk}~p^k(1-p)^{n-k} \\ = \sum_{k=1}^n {}_n\mathrm{C}_k~(pe^{t})^k~q^{n-k} = (q +pe^t)^n
$$

なので、ここから芋づる式に期待値と分散は、

* 期待値
$$
E[X] = \frac{\mathrm{d} }{\mathrm{d} t}M_X(0) =npe^t(q+pe^t)^{n-1}|_{t=0} = np
$$

* 分散
$$
E[X^2] = \frac{\mathrm{d^2} }{\mathrm{d} t^2}M_X(0) = \frac{\mathrm{d} }{\mathrm{d} t} npe^t(q+pe^t)^{n-1} \\ = npe^t(q+pe^t)^{n-1}+n(n-1)p^2e^{2t}(q+pe^t)^{n-2} |_{t=0} \\ = np + n(n-1)p^2 = n^2p^2 - np^2 + np
$$
$$
\therefore Var[X] = E[X^2] - E[X]^2 \\ = n^2p^2 - np^2 + np - n^2p^2  = np(1-p)~~~(= npq)
$$

となりますね！

# 幾何分布

これもベルヌーイ試行を考えます。
先ほどの二項分布では、Hの生じた回数をカウントしていたわけですが、
今回は、Hが１回生じるまでにかかる試行回数をカウントしましょう。
試行の度にカウンターを押し、Hが出たときのカウンターの数値がk となっている確率は、
k-1 回Tが出て、その次にHが出ればいいわけですから、

$$
Pr(X=k)=p(1-p)^{k-1} ~~~ (= pq^{k-1})
$$

と簡単に求まります。これが $ k : 1 \to \infty $ まで足し合わせると１になるのは読者への(ry
概形はこんな感じになります。もちろんのことながら、右下がりの指数関数ですね。

これも期待値と分散を求めましょう。
もちろん！モーメント母関数を求めますと、

$$
M_X(t)=E[e^{tX}]= \sum_{k=1}^\infty e^{tk}p(1-p)^{k-1} \\
= \frac{p}{q}\sum_{k=1}^\infty (qe^t)^k = p\cdot \frac{e^t}{1-qe^t}
$$

となりますから、ここから期待値と分散は

* 期待値
$$
E[X] = \frac{\mathrm{d} }{\mathrm{d} t}M_X(0) = p\cdot\frac{e^t(1-qe^t)+qe^{2t}}{(1-qe^t)^2} = p\cdot \frac{e^t}{(1-qe^t)^2}|_{t=0}=\frac{1}{p}
$$

* 分散
$$
E[X^2] = \frac{\mathrm{d^2} }{\mathrm{d} t^2}M_X(0) = \frac{\mathrm{d} }{\mathrm{d} t} \left( p\cdot\frac{e^t}{(1-qe^t)^2}\right) \\
= p \cdot \frac{(1-qe^t)^2~e^t + 2qe^{2t}(1-qe^t)}{(1-qe^t)^4} \\
= p \cdot \frac{(1-qe^t)~e^t + 2qe^{2t}}{(1-qe^t)^3} |_{t=0} = p \cdot \frac {p+2q}{p^3}=\frac{2-p}{p^2}\\
$$
$$
\therefore
Var(X) = E[X^2]-E[X]^2 = \frac{2-p}{p^2} - \left( \frac{1}{p} \right )^2 = \frac{1-p}{p^2}
$$

となりますね。

さて、ここで幾何分布の無記憶性を示しておきましょう。
無記憶性というのは「今までの結果はこれからのことに影響しない」ということです。
数式で書くと、条件付き確率で

$$
\forall n,k \in \mathbb{N}~~Pr(X > n+k|X > n) = P(X > k)
$$

と書けます。これに代入するために、$Pr(X > k)$を求めておきましょう：

$$
Pr(X > k) = 1 - \sum_{i=1}^{k}p(1-p)^{i-1} \\
= 1 - p\cdot\frac{1-q^{k}}{1-q} = 1- (1-q^k) = q^k
$$

簡単ですね！てなわけで、無記憶性の数式に代入すると、

$$
Pr(X > n+k|X > n) = \frac{Pr(X > n+k \wedge  X>n)}{Pr(X > n)} \\
= \frac{Pr(X>n+k)}{Pr(X>n)} = \frac{q^{n+k}}{q^n} = q^k = Pr(X>k)
$$

となり、確かに「過去のことなんか、関係ない！」となります。

# どんなことに使えるか

これら２つの分布の大本はベルヌーイ試行です。つまり、「YES or NOな現象」です。
ですから、
* 繰り返し行われる
* 独立である
* 確率は一定である
* その結果がデジタル値(0か1か、YESかNOか、HかTか）
ならば、上２つの分布がなりたつと考えていいでしょう。

ex1)
商店街のイベントで電子くじ引きをすることに決まった。
電子くじ引きは当たりか外れかのどちらかが一定の確率で出るとする。
「どうせなら」ということで、当たりは一度出たらくじ引きは終了とし、
その代わり、景品を（しょぼくれた商店街のくせに）ハワイ旅行にすることに。
もちろんのことながら、すぐ当たられては商売上がったりである。
そこで、100人より多いところで当たりが出る確率が
i) 90%になる当たりの確率 p とそのときの期待値
ii) 95%になる当たりの確率 p とそのときの期待値
iii) 99% になる当たりの確率 p とそのときの期待値
を求めてほしい。

ex2)
商品のとある機械は、1ヶ月に1度のメンテナンスで一定の割合である部分の故障が見つかる。
うちの方針で、必ずこちらが修理代を負担することになっている。
i) 今月、50台の機械をメンテナンスしたところ、4台が故障していた。
これは、今までのデータを見る限りごく平均的な故障台数である。
機械１台が次の月に故障している確率 p を求めよ。

ii) こんなにしょっちゅう故障されては、修理代のせいで赤字になってしまう。
そこで、会議の末、「２年保証」にすることにした。
つまり、なんとか故障確率を下げて、２年まではもつようにすればいい。
そこで、２年経つまでは故障しない確率が90%になるような故障確率を求めてほしい。

iii) 改善が達成したとき、修理代が1回10万円かかるとして、
1台、1年あたりの経費削減の見込みを求めてほしい。

iv) さらに、現在の機械保有者数は50人であり、これから保有者数が変わらないと仮定する。
また、故障確率を0.001下げるのに20万円の費用がかかる。
経費削減の分でこれを賄おうとすると、大体何年かかるか。


～解答～
ex1)
i) p = 0.00105305, 期待値 : 950人
ii) p = 0.000512801, 期待値 : 1950人
iii) p = 0.000100498, 期待値 : 9950人

ex2)
i) p = 0.08
ii) $p_{\mathrm{new}} = 0.0044$
iii) 90720円
iv) 3.3年

グレた確率統計

統計学の本は大体、二項分布から始まり、ポアソン分布、幾何分布、指数分布、…と次に分布の一覧をよこしてきます。
ただ、分布をたくさん与えられる（押し付けられる？）からといって、確率分布への理解が深まるとはあまり思えません。
 たしかに、期待値や分散の計算問題としては優秀ではありますが…それだけのために、ねえ？

大まかに分けて、「確率と統計」は２つの道に進めると思います。
ひとつは、正統派な統計の方。推定とか検定に繋がる道です。こっちの道の主役は正規分布、t分布、χ2分布などなど…。実践的な推定や検定へとつながっていきます。
もうひとつは、「統計」らしからぬ（？）方で、指数分布、ガウス分布、ポアソン分布などが主役となります。 これはどんな道かというと、確率過程に繋がるであろう道です。待ち行列とかですね。 人によっては、統計の道よりもこの確率過程の道をガンガン進んだほうが楽しく、有用かもしれません。
（ツールとしての統計学においては、変に深く数学的基礎をやるよりは、さっさと推定・検定をエクセルとかRを使いながらざくざくやっていく方がいいかもしれないわけです。途中で詰まってしまうくらいなら！）

というわけで、おそらくどこかにそのようなテキストはあると思いますが、備忘録がてら、数回に分けてそれについて書いていこうかなと思うわけです。

なんかすごいのの練習とamong理論のメモ

http://www.codecogs.com/eq.latex?数式(TeX) で、それ相応の画像が出力されるというのを見つけたので、テストテスト
ただし、代替の場合 \ はURL内で無効っぽいので、%5C にする必要があるっぽい

メレオロジー参考：　http://211.1.212.79/jalop/japanese/ronbun/2003/saito.pdf
codecogs参考： http://d.hatena.ne.jp/Zellij/20130103/p1

----
※ XAYのことを、「XはYについてamongである」「XはYについてamongなもの」とか訳します。


(E)

「どんな複数変項についても、かならずamongなindividualが存在する。」
これは集合と大きく違うところで、いわゆる『空複数』なんてものは存在しないということ。
集合は要素ゼロ（すなわち空集合)なものもあるが、複数変項にはそんなものが存在しない。
なぜなら、複数変項はそれ自体に実体はないからだ。
集合は「集合」というひとつの（数学的）単数的実体であるため、内部構造がnullでも存在しうる。

(AX1)

「XはYについてamongであるとは、XについてamongなすべてのindividualそれぞれがYとamongであるということ。」
amongの第一項（左側）は分配的だということ。


「Xがindividualであるとは、Xとamongなあらゆる複数変項Yについて、XはYについてamongであるということ。」



「XがYと同じ(the same things)とは、XとYが互いにamongであるということ。」


「XはYと被っている(overlap)とは、XともYともamongな複数変項Zが存在するということ」

（M1)

「amongは推移律を満たす」
かな？

（M2)

「XとamongなWすべてがYと被っているならば、XはYとamongである」

（弱補足性：weak supplementation principle）

「XはYとamongだが、YはXとamongでない場合、YにはXとamongでない部分がある」


Theorem
T1

反射律(推移律から明らか)

T2(強分配性)


Extensionality 1


Extensionaliti 2


T3


T4